Once the second hermit catches the disease, he visits another hermit. Besides himself, there are five hermits, only one of which is immune. If he DOES NOT visit that one immune hermit (probability=4/5), the disease is passed to a third hermit. That hermit, in turn, visits another hermit. If he visits one of the three NON-IMMUNE hermits (probability=3/5), the disease is passed to a fourth hermit. If he, then, visits one of the two NON-IMMUNE hermits (probability=2/5), the disease is passed to a fifth hermit. If the fifth hermit visits the only remaining NON-IMMUNE hermit (probability=1/5), the disease is passed to the sixth hermit. There are, now, no more hermits to be infected, so the outbreak ends with all six hermits infected.
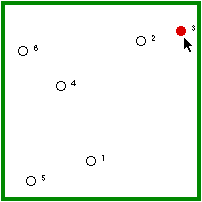
| Hermit #3 randomly gets the disease. | He randomly visits another hermit, who cannot be immune yet. |
 | 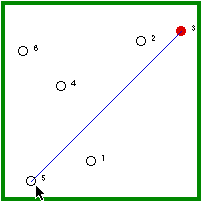 |
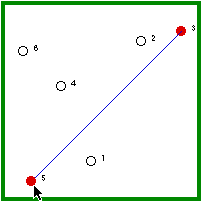
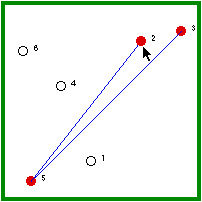
| Hermit #5 is randomly visited and, because he is not immune, he gets the disease. | Hermit #5 randomly visits a non-immune hermit (4/5 chance). |
 | 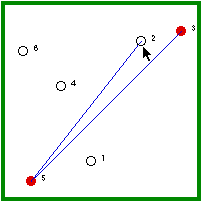 |
| Hermit #2 is randomly visited and, because he is not immune, he gets the disease. | Hermit #2, then, randomly visits another non-immune hermit (3/5 chance). |
 | 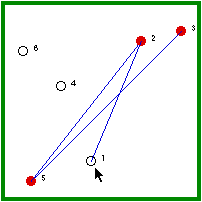 |
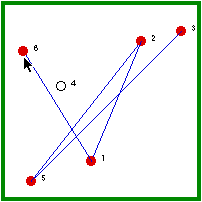
| Hermit #1 is randomly visited and, because he is not immune, he gets the disease. | Hermit #1, then, randomly visits a non-immune hermit (2/5 chance). |
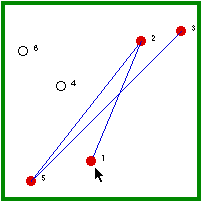 | 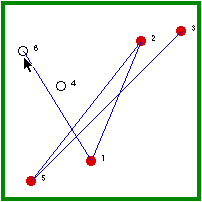 |
| Hermit #6 is randomly visited and, because he is not immune, he gets the disease. | Hermit #6, then, randomly visits a non-immune hermits (1/5 chance). |
 | 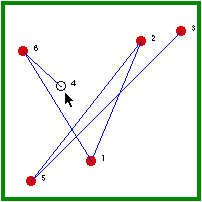 |
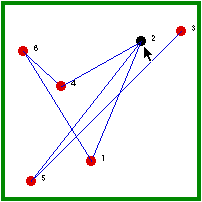
| Hermit #4 is randomly visited and, because he is not immune, he gets the disease. | Because all of the hermits have been infected, hermit #4 must visit an immune hermit (5/5 chance) and, thus, the outbreak ends. |
 |  |











