Four Infected Hermits

Each circle represents a hermit. Each red circle represents a hermit who gets the disease. Blue lines are drawn as one hermit visits another. If a hermit turns black, he has been visited twice and the disease ends.

Once the second hermit catches the disease, he visits another hermit. Besides himself, there are five hermits, only one of which is immune. If he DOES NOT visit that one immune hermit (probability=4/5), the disease is passed to a third hermit. That hermit, in turn, visits another hermit. If he visits one of the three NON-IMMUNE hermits (probability=3/5), the disease is passed to a fourth hermit. If he, then, visits one of the three immune hermits (probability=3/5), the outbreak ends with four infected hermits.
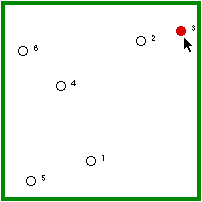
Hermit #3 randomly gets the disease.	He randomly visits another hermit, who cannot be immune yet.

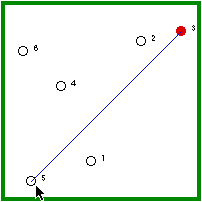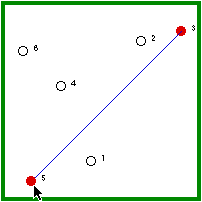
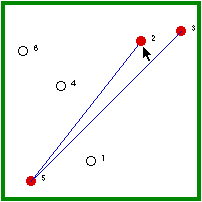
Hermit #5 is randomly visited and, because he is not immune, he gets the disease.	Hermit #5 randomly a non-immune hermit (4/5 chance).

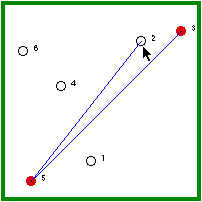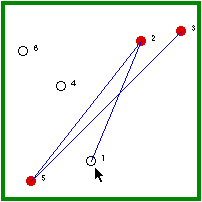
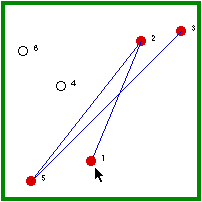
Hermit #2 is randomly visited and, because he is not immune, he gets the disease.	Hermit #2, then, randomly visits another non-immune hermit (3/5 chance).

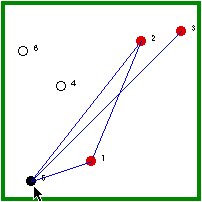
Hermit #1 is randomly visited and, because he is not immune, he gets the disease.	Hermit #1, then, randomly visits one of the other immune hermits (3/5 chance) and the outbreak ends.

The probability that exactly four hermits get sick = (The probability that the second hermit visits a non-immune hermit) · (The probability that the third hermit visits a non-immune hermit) · (The probability that the fourth hermit visits an immune one) = (4/5) · (3/5) · (3/5) = 36/125 = 0.2880

Return to the analytical solution.

Or continue to the explanation page for 5 infected hermits.