Two Infected Hermits

Each circle represents a hermit. Each red circle represents a hermit who gets the disease. Blue lines are drawn as one hermit visits another. If a hermit turns black, he has been visited twice and the disease ends.

Once the second hermit catches the disease, he visits another hermit. Besides himself, there are five hermits, only one of which is immune. If he visits that one immune hermit (probability=1/5), the disease ends with only two infected hermits.
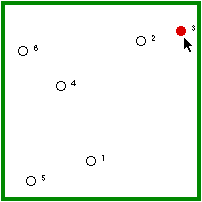
Hermit #3 randomly gets the disease.	He randomly visits another hermit, who cannot be immune yet.

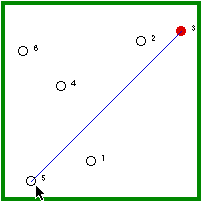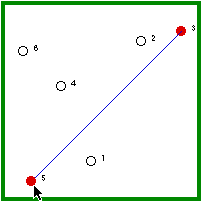
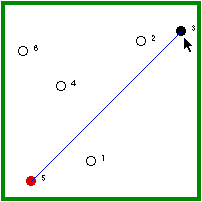
Hermit #5 is randomly visited and, because he is not immune, he gets the disease.	Hermit #5 randomly revisits #3 (1/5 chance) and, because #3 is immune, the disease outbreak ends.

The probability that only two hermits get sick = (The probability that the second hermit visits the only other immune hermit) = 1/5 = 0.2000

Return to the analytical solution.

Or continue to the explanation page for 3 infected hermits.