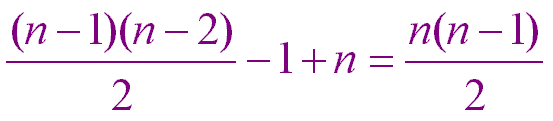Tips:

The Handshake Problem

In this problem there are a certain number of people in a room. If all of them shake hands, how many total handshakes took place?

Here is a challenge for middle school students interested in algebra. See if they can take the formula for the number of diagonals and add the variable n to the expression, then simplify the expression to get the expression for handshake problem.

That is, show that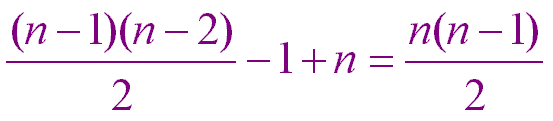

Time Estimate	Activity	Main Idea
20 min (3:00)	Investigate the number of diagonals in a polygon. Again, start with regular polygons.	Find the pattern.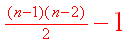
45 min (3:45)	The handshake problem.	Applications of this type of pattern. The formula to find is: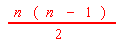

Step-by-step guide:

1. Have participants draw diagonals connecting the vertices of polygons

2. Discuss whether it makes a difference to the number of diagonals if the polygon is regular, convex, or concave. It makes no difference.

3. Have the participants fill out the table with the number of sides and the number of diagonals and find the pattern

4. Find the pattern for the number of diagonals plus the number of sides. This formula is the answer to the handshake problem. (See the sidebar at left).

Possible Problems and Concerns:

• Not all patterns are linear. This pattern may be harder to see than the others.
• With this problem the patterns become more complex. Allow time for participants to experiment and discuss this.
• It is important to take stock of where the progress at this point. We began with polygons and sides, and now we have complicated nonlinear expressions! We have discussed limits, discrete values, graphing, using variables and formulas. We are doing lots of algebra!