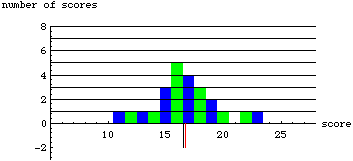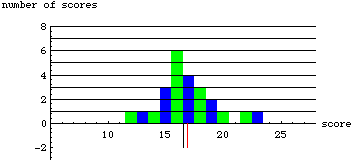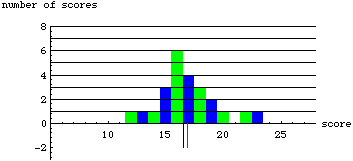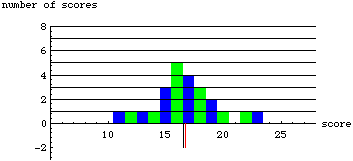
As you can see, the median does not change as long as the number of scores on either side of it stays the same. The mean, however, takes into account the distance of each score... each score has weight. Thus, if a score is moved far away from the mean, it will pull the mean in that direction.

You can think of the mean as the base of a see-saw. In order to balance the see-saw, it must move toward the objects that are farther away. Where the mean is depends upon both the amount of scores on each side of it and the distance of the scores from the mean.

Because the median is resistant to change, we call it a "robust" measure. Highly deviant scores (called "outliers") have no more effect on the median than those scores very close to the middle. However, as seen in our experiment with the dice data, outliers can greatly affect the mean.

If you have Excel, make sure you download the spreadsheet and fiddle with the scores. Your results should be even more convincing than the histograms provided here.

Please continue to the next page.

send comments and questions to Jay Hill