JIM DILDINE’S CALCULATOR PROGRAMS

Several years ago, I was just learning to program the TI brand of calculators and for fun I chose to focus on a few mathematics ideas. These programs can be used by anyone who would like to use them to enhance the opportunities for their students to learn these topics.

They encompass a few different ideas that are typically encountered in the Mathematics Curriculum. I will make recommendations as to where they might possibly fit in a typical Mathematics curriculum. You are free to modify these programs as needed provided you maintain the title splash screen. I will eventually turn these into a comprehensive suite with more menu options and the ability to import data to lists for analysis.


First, Prime Factors:


The concept of factoring down to a number’s prime factors is a crucial concept in pre-algebra and algebra. This program may help students understand and build factor trees for integers that they enter when prompted. Students should be familiar with the following table prior to using the program. Students should also create a factor tree of several numbers that they wish to factor.

Divisible By:

Divisibility Test:

Example:

2

Number ends in an even digit (0, 2, 4, 6, 8)

9,458 (ends in 8)

3

Sum of the digits are divisible by 3

8,751 (8+7+5+1 = 21, divisible by 3)

4

Last two digits form a number divisible by 4

3,432 (32 is divisible by 4)

5

Number ends in 0 or 5

890 and 7,345 are both divisible by 5

6

Number is divisible by both 2 & 3

342 is divisible by both 3 and 2

8

Last three digits for a number divisible by 8

27,816 is divisible by 8 since 816 is divisible by 8

9

Sum of the digits is divisible by 9

76, 104 is divisible by 9 since the sum of the digits is 18 which is divisible by 9

10

Last digit is 0

Any number that ends in 0

12

Number is divisible by both 4 & 3

4,032 is divisible by 12 since it is divisible by both 3 and 4



Second, Pythagorean Triples:


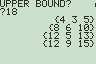
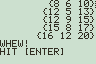
The Pythagorean Theorem (a^2 + b^2 = c^2) is an important concept in Algebra and Geometry. Knowing this relationship is very important throughout additional Mathematics areas as well. Pythagorean triples are the collection of an infinite many numbers that satisfy the Pythagorean Theorem. The user can use this program to examine a specific number of these triples. The user is prompted for an “UPPER bound”, that is the value that the program will use as the largest value for the largest of the legs. Students should be asked to discover relationships within these sets of triples. For example: (3, 4, 5) produces multiples (6, 8, 10) and (12, 16, 20) etc… Students should also realize that developing a list of Pythagorean Triples does not soely rely on multiples but a more comprehensive formula.



Third, Heron’s Formula for the Area of a Triangle:


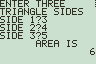
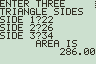
This program can be used in any math class that presents the formula for finding the area of a triangle. Typically students are given the standard triangle area formula Area = ½ Base x Height. This formula is a bit more complex but it allows the user to calculate the area of any triangle, given the lengths of its sides. Three examples are shown above: One that could have been calculated using the standard area formula, one that would have been a bit more difficult with the standard form but Heron’s Formula solves it for us, and one that determines that the given values do not fulfill the triangle inequality theorem which is an extension which may be explored.