
METHODOLOGY
Does technology-intensive instruction help high performing and low performing middle school mathematics students learn mathematics, improve their attitudes toward mathematics, explore mathematics in dynamic ways?
Can hand-held calculator technology help low performing and high performing middle school students identify mathematics?
To answer these questions a basic math class and an algebra class were instructed in mathematical concepts to examine how they would respond to technology intensive instruction. A study involving instruction, data collection, and analysis was developed to explore the issues surrounding the research questions and issues associated with them. The next sections are devoted to describing the methods of data collection, classroom instruction, equipment used, and data analysis.
To approach these questions a two-week unit using the TI-82 graphing calculator and the CBR distance sensor/motion detector was designed for two middle school classes. Data collection methods utilized to examine each class were-
The achievement tests were administered before and after the period of instruction.
The achievement tests consisted of ten multiple choice items taken from the Second International Mathematics Study that were meant to measure students' knowledge about the concept of rate, and reading and interpreting graphs. The test that was administered is included in Appendix B.
The attitudinal surveys were administered before and after the period of instruction.
The surveys consisted of 21 multiple choice items taken from the Second International Mathematics Study. The surveys were meant to gauge students' attitudes toward mathematics, and technology in the mathematics classroom. The surveys are included in Appendix A.
Interviews with four students from each class were conducted before and after the period of instruction. The interviews consisted of questions that were posed about the students' experiences in their current mathematics class, previous classes, their view of mathematics beyond the classroom, and their responses to questions about a graph (Appendix C) representing distance versus time. The eight students were chosen in cooperation with the classroom teacher to represent a range of the students in each class. This was done to collect and examine several snapshots of students who reflected several types of typical students in each class. Interviews were important to this study as that would be the most reliable method of establishing how significant the technology-intensive instruction had been to their understanding of the material and how they experienced or responded to the technology-intensive instruction.
Videotapes, audiotapes, and field notes were used to collect observations from daily classroom activities. Videotapes were made of three days of classroom instruction and audiotapes were used to record interactions between students on three additional days. Field notes were collected on each day of instruction. These extensive methods of data collection provided a comprehensive way to analyze every aspect of student performance, interaction, and exploration within the instructional experiences. Videotapes demonstrated student cooperation, student exploration through real-time data-collection, and student attempts that were not captured through audio means. Audiotapes collected student conversations within their groups and with the instructor to help in examining understanding at crucial moments of instruction. Field notes taken by the researcher collected subtle clues and hints of student exploration and provided the framework for what would become the student snapshots.
This study was conducted in a middle school in the Midwest. The data were collected in late November 1997 over a two-week period, of ten class sessions. The students attending this middle school are familiar with university students in education, and faculty from the university visiting their school and their classes. The regular classroom teacher assisted with the project to establish the best time of the school year and the classes that would be involved in this project. Two classrooms were chosen to reflect a range of students at the eighth grade level. These classrooms were a basic mathematics class, and an algebra class. The algebra class was the most advanced mathematics class offered at this school and the classroom teacher described the basic math class as consisting of low performing students that were frequently problematic in school.
Basic Mathematics
The basic mathematics class consisted of twenty-three students. The demographics for the basic math class are displayed in Table 1.
Table 1
Basic Math Demographics
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Algebra
The algebra class consisted of nineteen students. The demographics of the algebra class are presented in Table 2.
Table 2
Algebra Demographics
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The classroom teacher in this project assisted with the research design to involve the classrooms that would be most beneficial for the project and the students’ education. Research was conducted over ten class periods in each class. This amounted to a total of two weeks of instruction over ten course periods of approximately 50 minutes each (two days were shortened due to scheduling at the middle school).
The graphing calculators that were used in this research project were provided from Texas Instruments through their workshop loan program. The equipment was 7 Texas Instruments (TI-82) Graphing Calculators, one overhead display TI-82 model, and 6 Calculator Based Ranger devices (CBR).
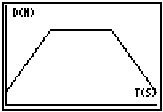
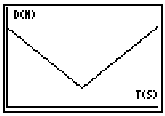
The CBR is a distance sensor or motion detector, a data collection device that can be connected to the TI-82 calculator through a simple link cable without special software, instruments, or wiring. This data collection device is a sonic motion detector that emits sonic waves in a conical (20-degree) formation with a range of 0.5 meters to 6 meters. The motion detector sends out an ultrasonic pulse and measures the time it takes for that pulse to return after being reflected back from the object whose distance you are measuring. (Texas Instruments, 1997) This data is used to create graphical representations of the object’s position. Some typical graphs created on the TI-82 by data collected by the CBR are included in Figure 1.



Figure 1. Graphs from a TI-82 created with the CBR unit.
Figure 1 depicts three graphs created from students' motion back and forth in front of the CBR unit. The first graph is a blank graph of distance (meters) vs. time (seconds). The second graph depicts a student who started about .5 meters away, walked away from the CBR, stopped roughly three meters away for about eight seconds, and then started walking back toward the CBR. The third graph depicts a student who started about three meters away from the CBR sensor, walker toward it, and then abruptly turned back and walked away from the CBR unit.
Heterogeneous groups consisting of four students were constructed in each class. The groups were chosen by a method using numbered cards and grouping all the students holding a certain number. These groups became permanent groups for the instructional period of two weeks. The groups of students participated in the activities with each other in order to fulfill the goals of the daily activity. There were smaller personal activities constructed and intended for individual completion outside of class. The classroom framework was constructed to provide the students with the opportunity to develop and experiment with the mathematical concepts while developing their own personal and group-negotiated conjectures. It was anticipated that during the instructional time the students would become investigators, and collaborators on the experiments, posing problems to one another and offering solutions within experiments and explorations.
The technology component of the research was constructed so the students would need to know very little about the equipment (The calculators and the CBRs). The technology component of this research project was designed to promote "learning through the technology not learning the technology" (PCAST, 1997, p.11). The ten days of instruction were not sufficient to allow for instruction of every facet of the calculators. Many of the students were about to use the calculator technology for the first time and some were apprehensive as to whether they would break them or in ruin the devices in some way. The lessons were designed to assuage possible student apprehension about the equipment.
It was important to instruct the students in the fewest steps necessary to operate the equipment for the instructional period.
In order to facilitate this aim, the students engaged in a brief introductory activity that enabled them to gain some familiarity with the calculators. The students learned three basic functions that would assist them in completing the activities. These functions were the ON, ENTER, and TRACE function keys.
A day-to-day outline of the activities and important questions from the instructional period follow.
Day 1
The first day of instruction was spent exploring the basic operations of the calculator equipment. Students were organized into groups to operate the ON, and ENTER keys and download the "Ranger" program from the CBR to the calculator. The surveys and achievement tests were administered as well, on this day.
Day 2
Students participated in matching randomly generated graphs. These graphs were generated from the calculator program and displayed on the screen. An example graph and a graph representing an attempt to match that graph by a student volunteer are presented in Figure 2.
Figure 2. Example graphs from the match-the-graph activity.
During the second day of instruction students were also expected to identify the axes and units on these axes.
Day 3 and Day 4
Students came to class with graphs they created at home to graph them on the equipment. They were expected to share these graphs and share instructions for creating them.
Students were then presented with a series of prompts/questions to interpret information from the graphs. Examples include-
Day 5
Students described the similarities between possible "real-world" graphs of distance vs. time (miles per hour) and the calculator generated graphs. Students also described other possible graphs of rate such as dollars per hour.
Day 6
Day six consisted of group presentations as the students were given an overhead sheet with a graph, blank graph area, and a series of questions on it or scenario to depict.
They were then expected to describe this scenario, answer some questions, and create the graph using the sensor in front of the class while presenting it on the overhead.
Day 7 and Day 8
The students attempted to trace specific data points on a graph; and give exact values (i.e., how far away from the sensor at specific time measures). Questions/prompts that were presented to the students were-
The students were expected to identify endpoints of intervals and determine the rate of change over that interval as best they could.
Day 9
The students reviewed concepts from the past few days. Topics of interest included-
Day 10
The last day was spent debriefing the students about their involvement in this project. Students were interviewed and the achievement tests were administered.
The intention of this research project was to answer the questions
Does technology-intensive instruction help high performing and low performing middle school mathematics students learn mathematics, improve their attitudes toward mathematics, explore mathematics in dynamic ways?
Can hand-held calculator technology help low performing and high performing middle school students identify mathematics?
Additional questions;
The data from achievement tests; surveys; interviews; and videotaped observations and were examined to observe the effects the technology intensive unit had on each class. The large amount data was analyzed to provide a detailed view into how the students responded to the activities and the technology during the instructional period. The analysis of this data is described in the next chapter.
The data were combined to produce a view of cognitive development during the instructional period, affective development toward mathematics, and cooperative interactions among group members. The intention was to see if the instructional period enhanced the students conceptual development, affective development, and cooperative interactions within the instructional setting especially those of the basic mathematics students.