a - the first term (extreme)
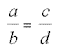
c - the third term (mean)
b - the second term (mean)
d - the fourth term (extreme)
James P. Dildine, 1999. jpd@wlsmail.com
This lesson offers an interesting high tech perspective on some really cool interrelated mathematics topics. Enjoy!
Every proportion (comparison of ratios) consists of four terms;
|
a - the first term (extreme) |
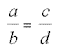 |
c - the third term (mean) |
|
b - the second term (mean) |
d - the fourth term (extreme) |
The product of the extremes will always equal the product of the means.
a * d = c * b
When a value is repeated in either the extremes or means as shown here
we get
x * x = z * y, or x^2 = y * z, or
and x is the geometric mean (mean proportional) of y and z.
Think: When asked to give the geometric mean of 3 and 12 you would arrange it like this.
and solve it like this.
3 * 12 = x^2 and
36 = x^2 and
x = SQRT(36) or
x = 6.
Think: Test it out with the following calculator and with your own calculations. Try some more here and experiment with various numbers.
Think: If the geometric mean is known, you can use it to find the value of another unknown in the proportion as is shown here.
|
6 |
|
12 |
|
12 |
x |
Think: In this case, the geometric mean is 12. How can you find the value for x?
The geometric mean isn't just fun but it can be quite useful too. It is especially useful in right triangles. Specifically triangles that are represented in the following figure.
Think: How many triangles do you notice in the figure?
Triangle ABC is a right triangle. So is triangle ACD, and triangle ABD.
The segment AD is an altitude (perpendicular segment, height) of triangle ABC.
Think: How can you prove that all three triangles are similar?
Since all three triangles are similar we can establish certain relationships among the sides. All the hypotenuses are similar, and all the legs are similar, even when they take on different characteristics.
|
AB is similar to CB |
|
We can then create a set of proportions using the ratios of pairs of corresponding sides.
Think: Does it look like the geometric mean is important here?
Think: Can you create three proportions displaying geometric means from the picture below (triangle with sides a,b, and c and smaller triangles with sides x, y, and h)?
Conclusions for this portion:
We can state with reasonable confidence that the altitude of the larger triangle is the geometric mean of the two segments of the hypotenuse of the larger triangle. or h is the geometric mean of x and y. or...
|
c |
|
h |
|
h |
y |
And,
|
a |
|
c |
|
x |
a |
|
c |
|
b |
|
b |
y |
Having Fun? Good! Go to the.......