Ahhh...Factoring...The Cornerstone of every Algebra Curriculum. The difference of two squares has always been a fascination for me, as this topic is not isolated within algebra but it is intrinsically geometric. Think about it: THE DIFFERENCE OF TWO SQUARES.

Difference = Subtraction

Squares = SQUARES, real geometric squares !!

Now the algebraic conclusion is drawn below:

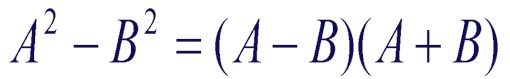
And then the geometric simulation is presented to allow the student to manipulate the geometric variables to see this resulted examined through many situations.

The geometric model depicts the subtraction of the area of the smaller square (B^2) from the area of the larger square (A^2) Otherwise known as A^2 - B^2. If you were to rearrange the area of the remaining region into a rectangle you would see that the areas illustrate the A^2 - B^2 = (A + B) (A - B) expression.

Sorry, this page requires a Java-compatible web browser.

I tried this once several years ago with lackluster results. The students tended to assign a numerical value to the construction paper examples they created as illustrated below. This does not necessarily illustrate the case for EVERY difference of two squares.

Cut out a square and name it "A" The area is A^2.

Next cut out another square from "A" and name it "B". This square's area is B^2.

 Remove (Subtract) square B from square A. and you have the measurements shown below.

Now, cut and rearrange the region "left-over" from square A.

 You will then have a rectangle with sides as shown.

 

The new rectangle has an area of L * W or in the case of our new region (A+B)*(A-B).