James P

James P. Dildine

CI 499 – Fall 2004

September 30, 2004

Pointy Fences

Creating a “Number 3” fence like the following with GeoFix Shapes leads us to see that we need 24 GeoFix shapes.

Now wait a minute, what about a “Number 1” fence or a “Number 2” fence?

Let’s see

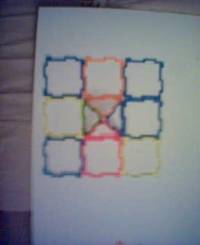
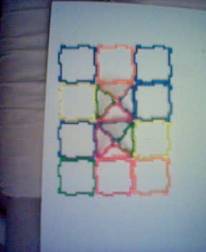
We see that there are 12 GeoFix Shapes in the “Number 1” fence.

And, 18 GeoFix Shapes in the “Number 2” fence.

Hmmmm….what type of pattern exists here?

Let’s make a chart while building “Number” fences:

Number of Fence Points	Number of GeoFix Shapes Needed
1	12
2	18
3	24
4	30

An example “Number 4” fence is shown here using 30 pieces.

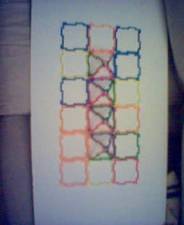
Hmmm, I notice that for each fence point I will need 6 shapes:

One on each side of the “point” and 4 shapes to create the pyramidal point. But….there are 6 extra pieces needed to form the boundaries.

That looks to me like (6 * the point + 6) would be a formula.

Let’s plug that into Excel:

With Excel we have the first 4

Number of Fence Points	Number of GeoFix Shapes Needed
1	12
2	18
3	24
4	30

And the last 4

Noticing that we need 606 GeoFix Shapes for a “Number 100” fence.

You are welcome to download the excel worksheet.

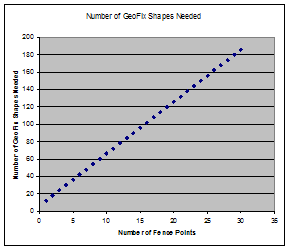
We can even graph it (this is up to 30 fence points):

And we can even extend this to include the possibility that each “fence point” has a base made of a GeoFix Shape.

This would give us the following chart and the accompanying formula:

Number of Fence Points	What if we created a base with a GeoFix Shape
1	13
2	20
3	27
4	34
5	41
6	48
7	55
8	62
9	69
10	76

7 * Number of points + 6

We can extend this in other ways as well:

What if we needed 2 rows of fences (to keep out marauders)?

What if we do not want any square pieces but a full range of pointy fences?