Agenda
Discuss Ancient Mathematical Tools: What Comes to
Mind?
Focus on: Abacus (Chinese) and Chisanbop.
Handouts Needed
Making an Abacus
Chisanbop
Materials
Abacus (Created or Bought)
Hands
Pencil
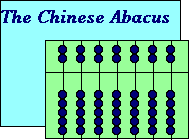
What is it? Look at the picture above.
Wooden rack of two rows of beads.
Rows are separated by a crossbar.
There are usually between 7 and 13 columns.
Each column has seven beads. Two in the top row "heaven" and
five in the bottom
row, "earth".
History:
Developed around 500-550 B.C.
Still widely used in Asia today.
What does an Abacus do?
Add, Subtract, Multiply, Divide in Base 10 (decimal
system)
Add and Subtract in Base 2 (Binary)
How do you use the abacus?
Assignment of numbers.
Each column is a power of ten. Much like our decimal
system.
Each column represents a power of ten
From left to right in a 7 column abacus
106 10 5 10 4 10 3
102 101 10 0
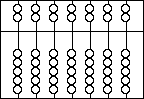
Each heaven bead is worth 5 * that power of ten
Each earth bead is worth 1 * that power of ten.
So the picture below represents the number 16. Ten is the
second column (one bead in earth used)
Five in the first column (One heaven bead used) and One in
the first column (One earth bead used).
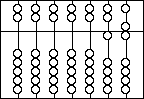
Adding: Try the following problem.
16+28
Start by setting up the abacus with the 16 as shown then
feed in the 28.
You should get this result
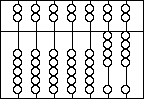
Subtracting: Try the following problem.
37-23
Start by setting up the larger number then clear out the
number you want to subtract.
Multiplying: Repeated Adding
Try the following
12*5 (Adding 12 five times of 5 is added 12 times)
How do you keep track of each addition sequence?
Try using another unused (prolly far right) column as a
tally column to keep a tally of each repeated sequence.
Dividing: Repeated Subtraction
Try the following
28 ÷ 4 (Taking four out of 28 how many times)
keep track of successive divisions same way as above.
What about larger numbers?
How would you go about Subtracting
3872 - 1624
Or Multiplying
12 x 12 without performing 12 additions?
Or 26 x 38?
Relevance to Primary and Secondary Level Educators
Help students develop a sense of numbers and their
meaning.
Tool to Aid in performing calculations.
Excellent for students who may still need physical
manipulatives as numbers are too abstract. Visually impaired
students love this device.
Give students a sense of ownership of the mathematics.
Easy to build and each student can make a powerful computing
device of their own.
Estimation is important in checking "right" answer.
Connection to history of mathematics. Mathematics was
created by people who used devices such as these.
Often a calculator is blamed for giving quick answers
without providing the knowledge necessary to understand
these answers. The abacus helps promote the process of
obtaining the answer.
Chisanbop
What is it? Literally, a hand-held calculator
requiring only the students' two hands.
History: Created by Korean teacher, Sung Jin Pai.
Basics: Each student holds out both hands palm-down and
makes two fists.
This represents zero. Now, extend all fingers. This
represents 99.
These are the maximum and minimum numbers of our
calculator.
The fingers of your left hand are each "worth" 10 and the
thumb is "worth" 50.
The fingers of your right hand are each "worth" 1 and the
thumb is "worth" 5.
Two thumbs extended equals 55. Two index fingers extended
equals 11.
Adding: Try 14 + 23
Subtracting: Try 27 - 18
Multiplying and Dividing: Try the problems presented for
use with the abacus and note difficulties and differences.
Relevance to Primary and Secondary Level Educators
Help students develop a sense of numbers and their
meaning.
Tool to Aid in performing calculations.
Excellent for students who may still need physical
manipulatives as numbers are too abstract. Visually impaired
students love this device.
Tool is readily available.
Gives students a sense of ownership of the
mathematics.
Estimation is important in checking "right" answer.
Often a calculator is blamed for giving quick answers
without providing the knowledge necessary to understand
these answers. Chisanbop helps promote the process of
obtaining the answer.
Focus Areas of Chisanbop and Abacus
Create and Solve 4 problems. One of Each operation on each
"Device"
Try to find some that make you develop a new technique.
Perform the calculation and detail your technique and
method.
Answer the following questions on a separate page.
How can these tools promote learning math for all?
How can students benefit from these methods?
Which Tool do you like best? Why?
What are some problems you can imagine with both
methods?
How can these problems be remedied?
Knowing what you know from Piagetian Theories of learning,
what benefits do you see with using tools such as these in
the Primary grades? What about secondary grades?